(13)
(14)
| 奈米晶粒材料 |
| 3. 超微顆粒 (Ultra-Fine Particles) | |
| 單獨超微顆粒的研究也許與奈米結構材料沒什麼太大的關係;就算奈米結構材料是由超微 | |
| 顆粒壓製而成,但在過程中的轉變也可能使其失去特殊的特徵。必須特別注意如第8節所指出, | |
| 細小顆粒的相轉變動力機制 (kinetics) 可能出奇的慢。研究單獨的顆粒之所以有趣是可以明白顯示 | |
| 固體熱力學上的「尺度效應」(size effect)。本文只討論單成分顆粒的效應。 | |
| 3.1 熔點降低 (Depression of the Melting Point) | |
| 我們早已知道小顆粒的熔點要比巨觀上的熔點低。如果固-液界面的曲度設為與顆粒表面一 | |
| 樣,根據式(9),可以得出一個單成分系統、半徑r的球狀顆粒之熔點的簡單表示: | |
| |
(13) |
| 其中Tm是正常巨觀下的熔點, |
|
| 驗的觀測也證實式(13)對小至~5 nm直徑的顆粒之預測都還算合理。如果再小的話, |
|
| 曲度的影響會太大。另外要怎麼認定「溶解」也不夠清楚。例如除了式(13)外,還可以採用尋找 | |
| 當固態與液態顆粒的自由能相等時的溫度。Buffat and Borel [13] 曾運用兩個模型的最精確形式來分 | |
| 析,但對小顆粒金(Au)的分析顯示,一直小到2 nm都看不出這兩個模型的差異。Figure 2 顯示實驗 | |
| 與模型預測非常一致。他們也考慮到小顆粒並非球形而是呈現出晶面的問題,並對模型做了必要 | |
| 的修正。大致說來,熔點降低的情形可以用下式表示: | |
| |
(14) |
| 其中的a,b等都是實驗常數。 | |
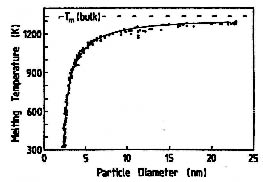 |
Figure
2. Au 顆粒的熔點是直徑的函數。實線是根據固態與液態顆粒具有相等自由能的模型計算求出。 |
| 3.2 小顆粒中的其他相 (Alternative Phases in Small Particles) | |
| 當固體顆粒夠小的時候,平衡狀態(自由能最低)並不一定是單晶。例如多雙晶顆粒 | |
| (multiply twinned particles)可以降低淨表面能,同時不會有小顆粒不能有的高應變能。多雙晶也會 | |
| 有好幾個不同的狀態,觀察發現小顆粒會不停而快速的(fluctuation)由一種狀態變化成另一種狀態 | |
| 。發生這種快速變化的範圍裡,很清楚的伴隨著不尋常高的熵,被稱為半溶解 (“quasimolten”) | |
| 狀態。經成核而形成這種狀態所花的能量要比維持這狀態高好幾個數量級。這種狀態與液態顯著 | |
| 不同,在顆粒半徑與熔解溫度的相圖中也有一定的區域(見Fig.3)。雖然相圖中顯示出系統的平 | |
| 衡狀態,但要注意(半溶解狀態除外)固態間的轉換可能受到kinetics的限制而保持在亞穩定狀態 | |
| (第八節)。Ajayan and Marks [17] 指出小顆粒狀態的重要性,例如薄膜的epitaxial生長在半溶解態 | |
| 與單晶態是連續時(如Fig.3)最為容易。 | |
| 似乎沒有雙成分或多成分超微顆粒的熱力學研究工作。但很可能這種顆粒之平衡會與平常 | |
| 的平衡相圖不同。例如:表面吸附某一種成分就會造成原本互溶的系統,形成實際上的不互溶。 | |
| 反之,原本會有相分離的合金,若顆粒直徑小於相互擴散的臨界波長 (critical wavelength,第6.1節 | |
| ,Figs. 7c and 8) 就顯現不出相分離。還有個例子,金屬間化合物 Ni3Al在超微顆粒時並不是化學 | |
| 性規則。如果規則相的表面能較不規則相高,則在小顆粒時平衡的會是不規則相。還有表面吸附 | |
| 也很重要,或規則化之kinetics也可能被阻礙(第8節)。仍有太多尚待研究。 | |
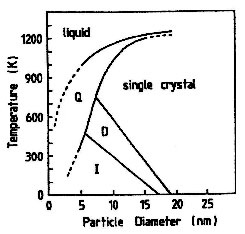 |
Figure 3. 計算得到之小顆粒金的相圖。其中包含測量之溶解溫度變化 (Fig. 2), 圖中除了液態與單晶外,並顯示出二十面體 (I, icosahedral)、十面體 (D, decahedral)、多雙晶顆粒與半熔解狀態 (Q)等的相場 (phase fields?)。 |
| 4. 奈米晶單相材料 (Nanocrystalline single Phase Materials) | |
| 原則上奈米結構材料的熱力學性質(相對焓、熵與Gibbs自由能)都可以直接測量(4.1節) | |
| 。以下描述量測的結果:由凝結與壓密製造的奈米晶粒金屬(4.2節)、機械研磨的奈米晶粒金屬 | |
| (4.3節)、和奈米晶粒陶瓷(4.4節)。 | |
| 4.1 熱與電化學量測 (Thermal and Electrochemical Measurements) | |
| 知道比熱當然可以計算一個系統任何狀態焓與熵的溫度變化。雖然材料的熵遵從第三定律 | |
| (有低溫數據的話可以計算),但這些量的絕對數值不能得知。通常最有趣的是焓、熵與 | |
| Gibbs自由能的差( |
|
 |
(15) |
| 其中最有趣的應該是奈米晶粒的熱力學函數與單晶間的差值;例如, |
|
| H(single crystal)。這樣由測量相變的熱,可以知道 |
|
| 不能得到 |
|
| 量溫度與熱量的方法並無法得出。 | |
| 電化學測量可以幫助定出絕對數量,因此重要。兩個標本的電極上勢能的差 |
|
| 其Gibbs自由能差 |
|
| |
(16) |
| 其中E1與E2是兩個樣本的電化學勢能(相對於參考電極), |
|
| ,n是金屬離子的電荷,F則是法拉第常數。 | |
| 4.2 緻密的與壓縮的金屬 (Condensed and Compacted Metals) | |
| 使用惰性氣體凝結法製造與壓製的奈米晶粒Cu, Pd與Pt的比熱[20, 21]都顯示大於正常大晶粒 | |
| 多晶質材料,甚至無晶質金屬。Pd奈米晶粒的超額量與其低密度有關。如果包括低溫比熱的測量 | |
| 值,超額比熱在整個溫度範圍內都與絕對溫度大致呈一線性關係: |
|
| = 0.026 J K-2 mol-1,Pd則h = 0.077 J K-2 mol-1。因為電子與磁性對比熱的影響都可忽略,超額比熱 | |
| (相對於單晶的比熱)可以歸因於在晶界上特別多出的振動熵與結構熵。最近研究顯示,Pt的超 | |
| 額比熱是由於其中存在的輕元素雜質。壓密至85%的材料在退火時的熱測量顯示出熱演化。又可 | |
| 分成兩期:第一期與不穩定晶界的鬆弛 (relaxation) 有關; 第二期則與晶粒生長有關。顆粒大小為 | |
| 12至18 nm的顆粒之總儲存熱焓約為 6.2 kJ mol-1,對照晶界超額熱焓在鬆弛前的約 ~2 J m-2與鬆弛後 | |
| 的約 ~1 J m-2,後者的值則與一般接受粗顆粒Pt的值相似。晶界上幾乎沒有超額熵,它們的超額 | |
| 自由能都是熱焓。 | |
| 凝結與壓製成的奈米晶粒Cu, Ni,與Pd的初步e.m.f.數值已被求出。一般說來,單晶與多晶的 | |
| E值並沒差別,但與奈米晶則有很大差異。因為內部並未達到平衡,因此多晶與奈米晶的e.m.f.量 | |
| 測有很大的問題。由 |
|
| 大顆粒多晶物質所測量之原子平均 |
|
| 就不正確了。晶界上的原子可能比在顆粒中的更為活動,所以可能會主宰了電化學測量的結果。 | |
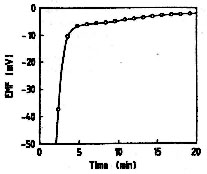 |
Figure
4. |
| 早期的e.m.f.量測,使用水溶液電解質,顯示雖然在室溫下奈米晶粒標本要比大顆粒多晶不 | |
| 穩定,但在較高的溫度此穩定度會反過來。這可以表示晶界在高溫的穩定效應 (stablizing effect) , | |
| 而且有人認為這可能是因為在晶界的原子具有超額熵的關係。但這結果與熱和構造測量所顯示的 | |
| 奈米晶粒材料在高溫會產生結晶生長的結果不合。也有人提出假說,認為這些測量是被某些特別 | |
| 活動的晶界原子所主導,並不能代表全部的晶界原子。最近的e.m.f.測量結果使用fused salt | |
| electrolyte ,可以完美解釋近來才測得的比熱與熱焓數值。尤其是發現Pd奈米晶粒在613至693 K會 | |
| 得到負的e.m.f.差值,表示即使在高溫奈米晶體也是較不穩定的。Fig.4中顯示隨著時間,奈米晶粒 | |
| 與大顆粒多晶的e.m.f.差值也漸漸減少。這與熱焓的量測結果一致,奈米晶的變化可分成兩個時期 | |
| ,第一個時期與晶界的鬆弛有關,第二個時期則與顆粒粒徑加大有關。Gartner估計奈米晶粒Pd伴 | |
| 隨鬆弛晶界的超額自由能,數值由當顆粒 ~20 nm的~1.0 kJ mol-1直到當顆粒 ~11 nm的~6.7 kJ mol1 | |
| ,相當於超額晶界自由能 ~1 J m-2。這些數值與超額熱焓的數值非常吻合。 | |
| 至少對顆粒粒徑小到 ~10 nm的情況,我們可以總結如下:奈米晶粒純金屬的晶界性質與大 | |
| 顆粒多晶時並無不同。奈米晶樣本的大晶界面積造成主要由熱焓產生之明顯的超額自由能。晶界 | |
| 上沒有發現任何entropy-stablization效應的證據,因此對奈米晶粒材料而言也不會有這種效應。 | |
| 4.3 機械式磨碎的金屬 (Mechanically Attritted Metals) | |
| 使用高能量球磨法以機械研磨的方式也可以製造奈米晶粒材料。正如同在凝結與壓製法製 | |
| 造的奈米晶粒材料一樣,測量其比熱也會顯現出增強效應。大多數的研究都是h.c.p.與b.c.c.金屬, | |
| 最近則發現這方法也可以製造c.c.p.金屬,因此可以直接與惰性氣體凝結法所製造的材料來比較。 | |
| 已知這方法所能得到的最小粒徑與融化溫度Tm與bulk模數B有關。達到理想的顆粒大小與累積高 | |
| 差排密度有關,因此若能阻止其回復 (recovery) 過程則可增進研磨的效果。最小粒徑由Al(低 | |
| Tm與低B)的 ~ 22 nm到Ir (高Tm與高B)的 ~ 6 nm。繞射研究顯示了顯著的rms晶格應變,同樣 | |
| 的也與Tm與B有關,由Al的 ~ 0.2% 到Ir的 ~ 0.9%。預期其高密度差排(這一點與凝結和壓製的不 | |
| 同)會對性質有重大影響。Eckert等人的研究認為差排密度是造成rms晶格應變的主因。其儲存的 | |
| 熱焓比起傳統變形材料大很多,從佔Ir熔化熱的 ~ 11%到Al的 ~ 43% 。在約0.4 Tm溫度範圍之退火 | |
| 研究顯示,所儲存的能量是因為回復作用、再結晶作用與晶粒成長作用而釋放出來。研究結晶生 | |
| 長的熱,得到晶界超額熱焓;Ni 約為 ~ 3 J m-2 (大約為完全鬆弛晶界的兩倍),Pd約為 ~ 1 J m-2 ( | |
| 約和大顆粒高角度晶界的值相當)。奈米晶粒Ni的晶界之所以不會鬆弛,可能與觀察到較低的晶 | |
| 粒生長活化能有關。Pd則與惰性氣體凝結Pt(由熱測量)和Pd(由電化學測量)的測量結果非常 | |
| 一致(見4.2節)。 | |
| 最容易在機械研磨中發現的高密度差排會在第9.1節討論。而在這些奈米結構材料的超額空 | |
| 孔密度(第9.2節)也會對熱力學性質產生影響。 | |
| 奈米晶粒材料也可用蒸發或濺鍍法製成薄膜。電化學測量指出濺鍍奈米晶可能與凝結壓製 | |
| 材料類似。最近,使用示蹤劑擴散法量測用電子束蒸發製造的奈米晶粒(5 nm)Fe,看不出來在 | |
| 凝結壓製材料所顯現的典型高擴散係數。雖然對蒸發材料並沒有熱力學數據,但測量擴散係數是 | |
| 個很好的警告─就算具有類似顆粒大小的奈米晶粒材料,其性質也可能因其製造方法而有很大的 | |
| 變化。特別要指出,凝結壓製材料預期具有較低的密度、更open的晶界與更大的原子傳輸速率。 | |
| 另外,不同程度的雜質可對熱力學性質造成重大的影響,特別是比熱。 | |
| 4.4 一種奈米晶質陶瓷 (A Nanocrystalline Ceramic) | |
| Chiang 等人研究由纖維狀SiC經化學分解而製成的奈米晶粒SiC,成分是單相正方晶系SiC , | |
| 顆粒粒徑~ 3 nm,但在晶界上有氧的雜質。液體熱量測 (solution calorimetry) 顯示超額自由能約在 | |
| 6到10 kJ mol-1的範圍,約等於晶界自由能0.25至0.5 J m-2。這些數值與前面討論的奈米晶粒Pd類似 | |
| (雖然它們可能被低估了)。有人認為晶界能的合理數值應為1至2 J m-2。晶粒生長時的熱量測 | |
| 顯示晶界熱焓為 ~ 3 J m-2。 |
|
| 到目前為止的討論,超額熱力學性質都主要與晶界相關。似乎都沒有考慮到像在式(3)中提 | |
| 到的晶界接線與晶粒尖角。可能是因為至今研究的材料粒徑仍不夠小,所以高次項的效應並未出 | |
| 現。 | |
| 5. 奈米相材料 (Nanophase Materials) | |
| 5.1 熔點降低 (Depression of Melting Point) | |
| 被一顆顆包裹在惰性氧化物的金屬顆粒,其熔化行為可能與單獨顆粒類似。Fig.5 顯示Bi被 | |
| 包裹在SiO2中其熔化溫度的變化。這情形與式(13)一致,即由固液界面的曲度所導致的熔化溫度 | |
| 降低。 | |
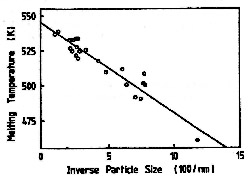 |
Figure 5. Bi被包裹在SiO2中時,其熔化溫度是粒徑大小的函數。樣本是granular 金屬薄膜,含有20至90% Bi。 |
| 當熔化的相為基質,其中含有惰性顆粒的不互融奈米相系統時,也會有熔點降低的現象。 | |
| 球磨之Sn/Ge混合即為一例。其中之Ge顆粒約10 nm 直徑,分散於Sn中;而Sn的熔點降低了約40 | |
| K。這樣的降低不能用式(13)來解釋,因為其界面曲率不能簡單定出。但是如果熔化的Sn所造成 | |
| 的Sn/Ge界面自由能要比結晶質Sn所造成的低,在此奈米相材料中的大界面面積(單位體積含A) | |
| 即可能降低平衡熔化溫度。令單位面積界面自由能的差為 |
|
| |
(17) |
| 其中的 |
|
| Tm得出很合理的 |
|
| 率增加,樣本的熔解熱焓降低,並在體積分率達到零之前就變成零。這可以用大約有一層接觸 | |
| Ge的Sn原子是非晶質的假說來解釋,符合的情況可以見Figure 6。嚴格說來,當用式(17)時V一定 | |
| 要為結晶質Sn的體積分率,不能包含非晶質的部份。熔化熱焓的提前消失(Ge體積分率還未到零 | |
| )是個明顯的例子,顯示即使只有一層界面相,只要界面密度夠高,對塊體性質的影響就會很重 | |
| 要。 | |
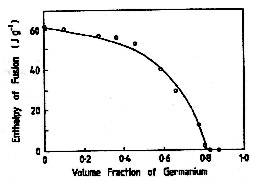 |
Figure
6. 球磨Sn(其中包含Ge顆粒)的熔化熱焓對Ge體積分率的函數。實線是由假設一層非晶質Sn與Ge界面接觸的模型所計算出來的。 |
| 5.2 溶解度增高 (Enhanced Solubility) | |
| 奈米相材料在實用技術上很引人興趣。例如兩相之金屬間(intermetallic)構造能有理想的機械 | |
| 性質,而且能抵抗晶粒長大。相與相間的作用顯然非常重要。詳細的研究都侷限於兩種元素的模 | |
| 型系統。例如:在Ag與Fe的奈米晶粒合金中,這兩種原本不互溶的元素顯示出增強的相互溶解度 | |
| 。這被解釋成是彈性應變的緣故,但在2.4節中所討論的增強溶解度也應一起考慮。 | |
| 5.3 應力效應 (Stress Effects) | |
| Cammarata and Eby指出,作用在奈米結構材料上的界面應力應該會對其中各相的晶格常數產 | |
| 生可以測量得到的效應。原則上,晶格可以擴張或被壓縮,預期應變可以大到~ 1%。界面應力對 | |
| 界面兩邊的相都是相同正負號,這與coherency效應不同。Cammarata and Eby分析微小薄層聚合體微 | |
| 構造,結果顯示晶格常數隨薄層厚度的倒數之線性變化與界面應力效應相符。其中界面應力如預 | |
| 期的與界面自由能大致相當,但有趣的是它竟是負值。這是由聚合體晶體表面若要發生chain- | |
| folding相當困難所致。 | |
| 奈米晶粒合金中的兩個相,非常可能具有不同的熱膨脹係數。所以溫度的變化就應該會導 | |
| 致應力。(正如coherency應力,這效應在兩相上會有彼此相反的正負號)。對熱膨脹差異 | |
| (mismatch)似乎並沒有詳細的實驗研究;雖然應力所產生的效應可能很重要,但若比起界面所產 | |
| 生的效應,其效應卻很清楚的較小。Granular Al,其中含有奈米相的Al與Al2O3混合,是個常見的 | |
| 顯示具有很大不同熱膨脹的相組合(Al的
|
|
| 生如一般界面應力所造成的約1%的應變差異,需要極不合理的~ 630 K溫度變化。 | |
| 單元七 |
單元八 |
單元九 |